Polynomials Class 10 Maths NCERT Solutions
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 2 Polynomials.
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.1
Question 1:
The graphs of y = p(x) are given below for some polynomials p(x). Find the number of zeroes of p(x) in each case.
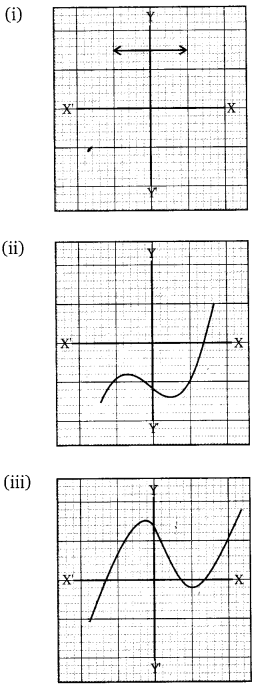
Solution:
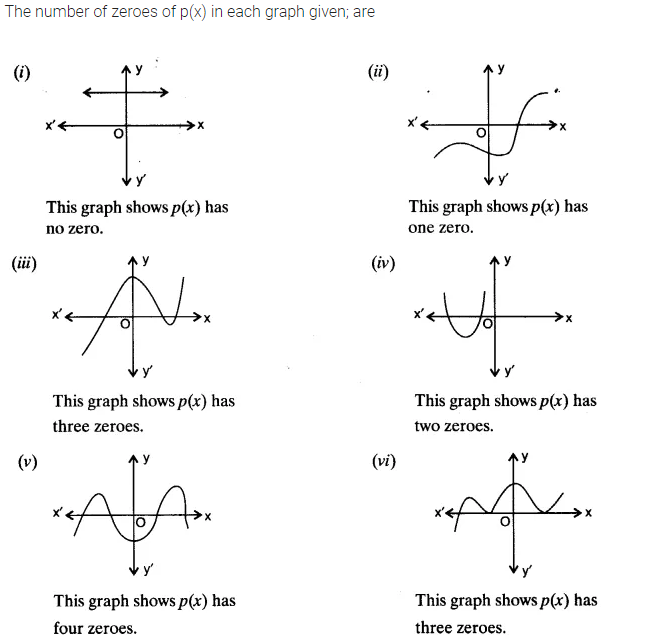
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.2
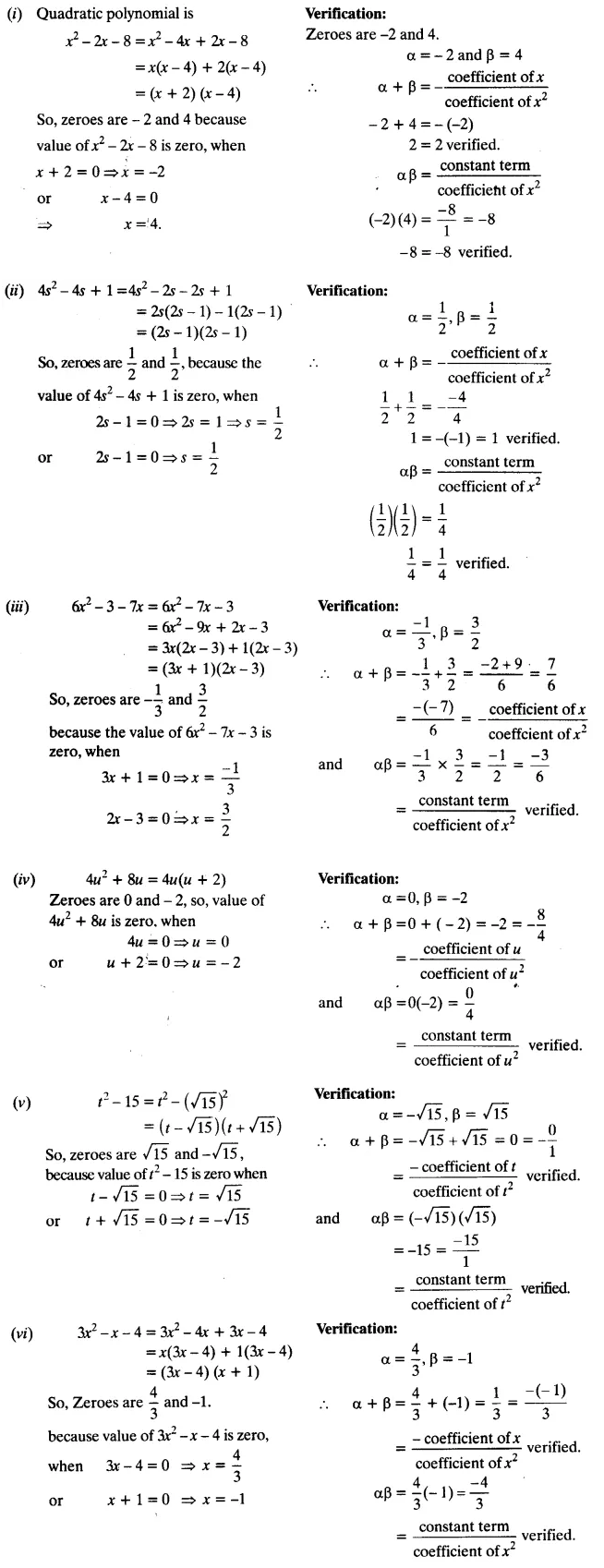
Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and their coefficients:
(i) x2 – 2x – 8
(ii) 4s2 – 4s + 1
(iii) 6x2 – 3 – 7x
(iv) 4u2 + 8u
(v) t2 – 15
(vi) 3x2 – x – 4
Solution:
Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively:
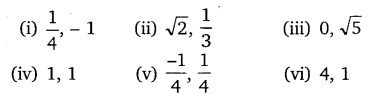
Solution:

Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.3
Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4– 5x + 6, g(x) = 2 – x2
Solution:

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t2 – 3, 2t4 + 3t3 – 2t2– 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x2 + 3x + 1, x5 – 4x3 + x2 + 3x + 1
Solution:

Question 3.
Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are and (sqrt { frac { 5 }{ 3 } }) and –(sqrt { frac { 5 }{ 3 } })
Solution:

Question 4.
On dividing x3 – 3x2 + x + 2bya polynomial g(x), the quotient and remainder were x – 2 and -2x + 4 respectively. Find g(x).
Solution:
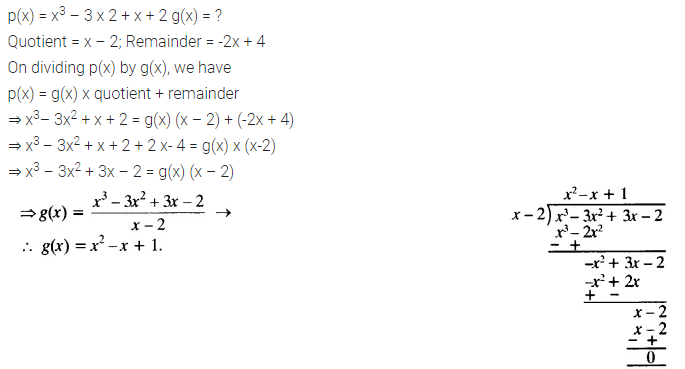
Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and:
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
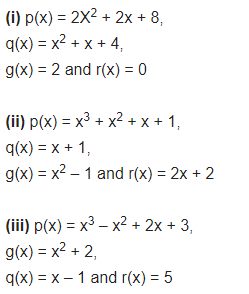
Class 10 Maths NCERT Solutions Chapter 2 Polynomials Ex 2.4
Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; (frac { 1 }{ 4 }), 1, -2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Solution:

Question 2.
Find a cubic polynomial with the sum, some of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:
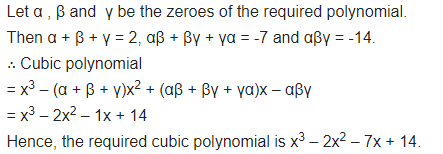
Question 3.
If the zeroes of the polynomial x3 – 3x2 + x + 1 are a-b, a, a + b, find a and b.
Solution:

Question 4.
If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± √3, find other zeroes.
Solution:

Question 5.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:

Class 10 Maths Polynomials Mind Map
Polynomial
An algebraic expression f(x) of the form
f(x) = a0 + a1x + a2x2 +…. + anxn,
where a0, a1, ……., an are real numbers and all indices of variables are non-negative integers is called polynomial in variable x.
(i) The highest power of x is called degree of the polynomial.
(ii) a0, a1x,….,anxn are terms of the polynomial.
(iii) a0, a1 ,….an are co-efficients of the polynomial.

Standard Forms of Linear, Quadratic and Cubic Polynomials
(i) Linear Polynomial:
ax + b, where a, b are real numbers and a ≠ 0.
(ii) Quadratic Polynomial:
ax2 + bx + c, where a, b, c are real numbers & a ≠ 0.
(iii) Cubic Polynomials:
ax3 + bx2 + cx + d, where a, b, c, d are real numbers and a ≠ 0.
Value of a Polynomial
The value of a polynomial f(x) at x = a is obtained by substituting x = a in the given polynomial and is denoted by/(a).
Zero(es)/Root(s) of Polynomial
x = r is a zero of a polynomial p(x) if p(r) = 0.
Geometrical Meaning of Zeroes of a Polynomial

Zero(es) of a polynomial is/are the x-coordinate of the point(s) where graph y = fix) intersects the x-axis.
(i) Linear polynomial: Graph of linear polynomial is a straight line and has exactly one zero.
(ii) Quadratic polynomial: Graph of quadratic polynomial is always a parabola and this polynomial can have atmost two zeroes.
(iii) Cubic polynomial: Cubic polynomial can have atmost three zeroes.
Cases of Quadratic Polynomial
Case-I : If a quadratic polynomial P(x) = ax2 + bx + c has two zeroes, then its graph will intersect the x-axis at two distinct points A and B as shown in the figure.

Case-II: If a quadratic polynomial P(x) = ax2 + bx + c has only one zero, then its graph will touch the x-axis at only one point A as shown in the figure.

Case-III : If a quadratic polynomial P(x) = ax2 + bx + c has no zero, then its graph will not intersect /touch the x-axis at any point as shown in the figure.

Relationship between Zeroes and Coefficients of a Polynomial
(i) Zero of a linear polynomial ax + b is x = (-frac{b}{a})
(ii) If α and β are the zeroes of the quadratic polynomial ax2 + bx + c, then
α + β = (-frac{b}{a})

(iii) If α, β and γ are zeroes of the cubic polynomial ax3 + bx2 + cx + d then

Division Algorithm
If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that p(x) = g(x) × q(x) + r(x)
where either r(x) = 0 or degree of r(x) < degree of g(x)
NCERT Solutions for Class 10 Maths
- Chapter 1 Real Numbers
- Chapter 2 Polynomials
- Chapter 3 Pair of Linear Equations in Two Variables
- Chapter 4 Quadratic Equations
- Chapter 5 Arithmetic Progressions
- Chapter 6 Triangles
- Chapter 7 Coordinate Geometry
- Chapter 8 Introduction to Trigonometry
- Chapter 9 Some Applications of Trigonometry
- Chapter 10 Circles
- Chapter 11 Constructions
- Chapter 12 Areas Related to Circles
- Chapter 13 Surface Areas and Volumes
- Chapter 14 Statistics
- Chapter 15 Probability
<!–
–>